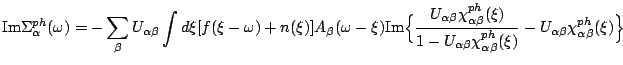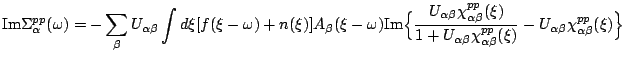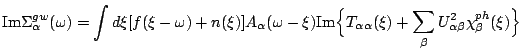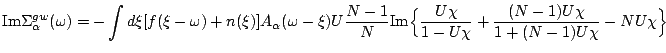Next: Running FLEX program
Up: FLEX_descrip
Previous: FLEX_descrip
Details of FLEX evaluation
The FLEX approximation sums up three different infinite classes of
diagrams, particle-particle ladder 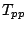 and two particle-hole
channels which can be grouped together into particle-hole T-matrix
and two particle-hole
channels which can be grouped together into particle-hole T-matrix
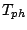 in the following way
in the following way
Here
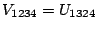 ,
,
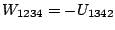 and polarization
diagrams are
and polarization
diagrams are
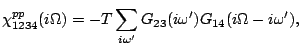 |
|
|
(3) |
 |
|
|
(4) |
We assumed here a scalar product of the form
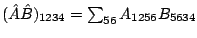 .
Finally the FLEX self-energy becomes
.
Finally the FLEX self-energy becomes
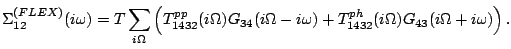 |
(5) |
The equations can be considerably simplified if the hybridization
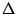 is diagonal and the Coulomb repulsion is of the form
is diagonal and the Coulomb repulsion is of the form
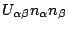 . In this case, propagators in the above equations are also
diagonal, i.e.,
. In this case, propagators in the above equations are also
diagonal, i.e.,
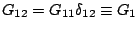 and the two
particle-hole channels do not mix anymore and can be separately summed
up. The two ladders become a simple geometric series and can be
explicitely inserted into self-energy expression
and the two
particle-hole channels do not mix anymore and can be separately summed
up. The two ladders become a simple geometric series and can be
explicitely inserted into self-energy expression
| |
|
![$\displaystyle \Sigma^{pp}_{\alpha }(i\omega )=T\sum_{\b }U_{\alpha \b }\sum_{i\...
..._{\alpha \b }(i\Omega )}-U_{\alpha \b }\chi^{pp}_{\alpha \b }(i\Omega )
\right]$](img19.png) |
(6) |
| |
|
![$\displaystyle \Sigma^{ph}_{\alpha }(i\omega )=T\sum_{\b }U_{\alpha \b }\sum_{i\...
..._{\alpha \b }(i\Omega )}-U_{\alpha \b }\chi^{ph}_{\alpha \b }(i\Omega )
\right]$](img20.png) |
(7) |
where the simplified polarisation diagrams are
| |
|
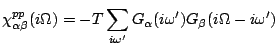 |
(8) |
| |
|
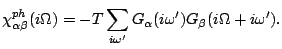 |
(9) |
The third GW channel can also be analytically summed up for the SU(N)
case, but if the crystal field splitting is assumed, one still needs to
solve a matrix equation
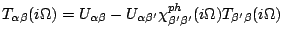 |
|
|
(10) |
to obtain the self-energy of this channel
![$\displaystyle \Sigma^{gw}_{\alpha }(i\omega )=-T\sum_{i\Omega }G_{\alpha }(i\om...
...\alpha }(i\Omega )+\sum_\b U_{\alpha \b }^2\chi^{ph}_{\b\b }(i\Omega )
\right].$](img24.png) |
|
|
(11) |
In the SU(N) case, the summation can be performed and the result is
![$\displaystyle \Sigma^{gw}_{\alpha }(i\omega )=-T\sum_{i\Omega }G(i\omega +i\Ome...
...i^{ph}(i\Omega)}-\frac{U}{1-U\chi^{ph}(i\Omega)}+N
U\chi^{ph}(i\Omega)\right].$](img25.png) |
(12) |
Somethimes it is more convenient to work on real axis and thus avoid
the problem of analytic continuation. The price one pays is that
the functions on real axis have more structure to resolve and the
equidistant mesh is in many cases too expensive. Therefore, it is
desired to work with nonequidistant meshes on real axes with more
points around zero frequency where Fermi function drops quickly and
most of sensitive structure is located. The FLEX equations can be
analytically continued to real axes by the standard contour
integration and the results is
In the SU(N) case, the last contribution can again be simplified to
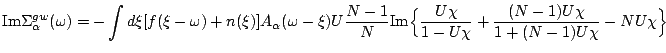 |
|
|
(19) |
Next: Running FLEX program
Up: FLEX_descrip
Previous: FLEX_descrip
Kristjan Haule
2004-08-23
![]() and two particle-hole
channels which can be grouped together into particle-hole T-matrix
and two particle-hole
channels which can be grouped together into particle-hole T-matrix
![]() in the following way
in the following way
![]() is diagonal and the Coulomb repulsion is of the form
is diagonal and the Coulomb repulsion is of the form
![]() . In this case, propagators in the above equations are also
diagonal, i.e.,
. In this case, propagators in the above equations are also
diagonal, i.e.,
![]() and the two
particle-hole channels do not mix anymore and can be separately summed
up. The two ladders become a simple geometric series and can be
explicitely inserted into self-energy expression
and the two
particle-hole channels do not mix anymore and can be separately summed
up. The two ladders become a simple geometric series and can be
explicitely inserted into self-energy expression
![$\displaystyle \Sigma^{pp}_{\alpha }(i\omega )=T\sum_{\b }U_{\alpha \b }\sum_{i\...
..._{\alpha \b }(i\Omega )}-U_{\alpha \b }\chi^{pp}_{\alpha \b }(i\Omega )
\right]$](img19.png)
![$\displaystyle \Sigma^{ph}_{\alpha }(i\omega )=T\sum_{\b }U_{\alpha \b }\sum_{i\...
..._{\alpha \b }(i\Omega )}-U_{\alpha \b }\chi^{ph}_{\alpha \b }(i\Omega )
\right]$](img20.png)
![$\displaystyle \Sigma^{gw}_{\alpha }(i\omega )=-T\sum_{i\Omega }G_{\alpha }(i\om...
...\alpha }(i\Omega )+\sum_\b U_{\alpha \b }^2\chi^{ph}_{\b\b }(i\Omega )
\right].$](img24.png)
![$\displaystyle \Sigma^{gw}_{\alpha }(i\omega )=-T\sum_{i\Omega }G(i\omega +i\Ome...
...i^{ph}(i\Omega)}-\frac{U}{1-U\chi^{ph}(i\Omega)}+N
U\chi^{ph}(i\Omega)\right].$](img25.png)
![$\displaystyle \mathrm{Im}\{\chi^{ph}_{\alpha \b }(\Omega )\}=\pi\int d\xi[f(\xi-\Omega )-f(\xi)]A_{\alpha }(\xi)A_{\b }(\xi-\Omega )$](img26.png)
![$\displaystyle \mathrm{Im}\{\chi^{pp}_{\alpha \b }(\Omega )\}=\pi\int d\xi[f(\xi-\Omega )-f(\xi)]A_{\alpha }(\xi)A_{\b }(\Omega -\xi)$](img27.png)