Hubbard I approximation
To be specific, we concentrate on the Anderson impurity Hamiltonian
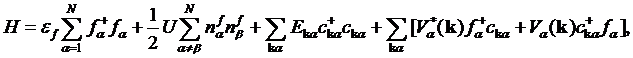(1)
describing the
interaction of the impurity level 
with bands of
conduction electrons 
via hybridization 
. 
is
the Coulomb repulsion between different orbitals in the 
–band.
Now we turn to
the Hubbard I approximation [1] which is closely related to the moments expansion
method [2]. Consider many–body atomic states 
which in 
are
all degenerate with index 
numerating these
states for a given number of electrons 
The impurity Green
function is defined as the average
(2)
and becomes
diagonal with all equal elements in . It is convenient to
introduce the Hubbard operators
(3)
and represent the one–electron creation and destruction operators as follows
(4)
(5)
The impurity Green function (2) is given by
(6)
where the
matrix 
is defined as
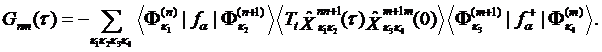(7)
Establishing
the equations for can be performed using
the method of equations of motion for the 
operators. Performing
their decoupling due to Hubbard [1,3], carrying out the Fourier transformation
and analytical continuation to the real frequency axis, and summing over 
and
after (6) we arrive to the main result
(8)
where
hybridization 
satisfies the DMFT
self–consistency condition of the Hubbard model on a Bethe lattice
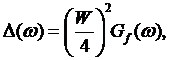(9)
with 
being
the bandwidth.
The 
can
be viewed in the matrix form (6) with the following definition of a diagonal
atomic Green function
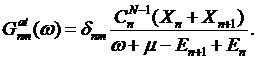(10)
with 
being
the total energies of the atom with electrons in 
The
coefficients 
are the probabilities
to find atom with electrons while
combinatorial factor 
arrives due to
equivalence of all states with electrons in .
The
coefficients are normalized to
unity, 
and are expressed via diagonal elements of 
as
follows:
(11)
Their
determination in principle assumes solving a non–linear set of equations while
determining 
The mean number of
electrons can be measured as follows: 
or as follows 
The
numbers can be also used to find the averages 
: density–density
correlation function for local states with electrons
is proportional to the number of pairs formed by particles 
.
Since the probability for electrons to be
occupied is given by: 
, the physical
density–density correlator can be deduced from: 
. Similarly,
the triple occupancy can be calculated from 
.
If we neglect
by the hybridization 
in Eq. (8), the
probabilities become simply
statistical weights:
(12)
We thus see
that in principle there are several different ways to determine the
coefficients , either via
self–consistent determination (11), or using statistical formula (12). To
determine the best procedure let us first consider limits of large and small ’s.
When 
, 
is reduced to 
i.e.
the Hubbard I method reproduces the atomic limit. Setting 
gives
, which is the correct band limit. Unfortunately, at half–filling
this limit has a pathology connected to the instability towards Mott transition
at any interaction strength .
0.6cm
[1] J. Hubbard, Proc. Roy. Soc. (London) A281, 401 (1964).
[2] W. Nolting, and W. Borgiel, Phys. Rev. B 39, 6962(1989).
[3] L. M. Roth, Phys. Rev. 184, 451 (1969).
Running program
· compile program typing "make" at the source files location. Makefile was tested on Linux OS using PGI compiler. Please adjust it depending on operating system and compiler used.
· Edit “input" file which has the following structure:
|
1 |
IMOD |
|
0.0 |
EF |
|
2.0 |
U |
|
0.016 |
TEMP |
|
4 |
NDEG |
|
500 |
NMSB |
|
500 |
OMAX |
|
500 |
NOMG |
|
50 |
WEND |
|
F |
COMPUTE_REAL |
where IMOD = 1 is the Hubbard Model, IMOD=3 the Anderson impurity model, EF is the impurity level, U is value of Coulomb repulsion, TEMP is temperature to be used used to create for Matsubara points grid, NDEG is the degeneracy, NMSB is the number of Matsubara point, OMAX is the imaginary frequency cutoff, NOMG is the number is real frequency points, WEND is the real frequency cutoff, COMPUTE_REAL is flag once is “True" tell program to produce the self-consistent solution (last iteration) on real axis.
1. Program’s input consists from one more file (provided the Anderson impurity model item is chosen in “input" file):
“delta.dat" containing the hybridization function.
The structure is the following:
|
Column # |
Value |
|
1 |
Frequency |
|
2 |
Re Delta |
|
3 |
Im Delta |
1. Run the program executable (“main" is the default name).
2. Program’s output consists from the following files:
1) “gfsig_iw.dat" containing Green’s function (GF) and the self-energy (SE) on Matsubara axis
2) “gfsig_re.dat" containing Green’s function (GF) and the self-energy (SE) on real axis provided flag "COMPUTE_REAL" is “TRUE".
They have the same structure:
|
Column # |
Value |
|
1 |
Frequency |
|
2 |
Re GF |
|
3 |
Im GF |
|
4 |
Re SE |
|
5 |
Im SE |
3) “grid_re.dat" containing real frequency grid for the hybridization function (delta).
4) “grid_im.dat" containing Matsubara frequency grid for the hybridization function (delta).
Both files have the same structure:
|
Column # |
Value |
|
1 |
Frequency |
Program content
|
Makefile |
main make file |
|
dmf_cmpdiag.f |
The solution of the generalized eigenvalue problem |
|
imp_sunatm.f |
Solves Anderson impurity model, returns GF and SE. |
|
lib_broy6.f |
Broyden mixing. |
|
lib_cinv.f |
Finds inverse of square matrix. |
|
lib_csplines.f |
Splines complex function from one to another grid. |
|
lib_deriv1.f |
Calculates radial derivative. |
|
lib_morefun.f |
Calculations of a few auxiliary functions |
|
lib_pade.f |
Realization of Páde procedure. |
|
lib_splin3.f |
Computed a natural spline approximation of third order. |
|
mod_common.f |
File containing common modules used across the program. |
|
mod_dimart.f |
File containing common modules used across the program. |
|
mod_init.f |
File containing common modules used across the program. |
|
sunhub1.f |
Main program. |