Interpolative Approach

We start with writing down the Anderson impurity Hamiltonian

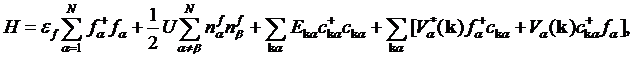                                (1)

 

describing the interaction of the impurity level  with bands of conduction electrons  via hybridization .  is the Coulomb repulsion between different orbitals in the –band. In order to solve the Anderson impurity model in general multiorbital case, we use a rational interpolative formula for the self–energy. This can be encoded into a form

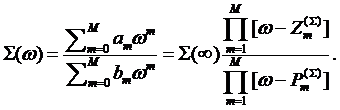                                                                                                         (2)

The coefficients , , or, alternatively, the poles , zeroes  and value of the self-energy at infinity  in this equation are to be determined. The form (2) can be also viewed as a continuous fraction expansion but continuous fraction representation will not be necessary for the description of the method.

Our basic assumption is that only a well distinct set of poles in the rational representation (2) is necessary to reproduce an overall frequency dependence of the self–energy. Extensive experience gained from solving Hubbard and periodic Anderson models within DMFT at various ratios of the on–site Coulomb interaction  to the bandwidth  shows the appearance of lower and upper Hubbard bands as well as renormalized quasiparticle peak in the spectrum of one–electron excitations.

It is clear that the Hubbard bands are damped atomic excitations and to the lowest order approximation appear as the positions of the poles of the atomic Green’s function. In the  symmetry case which is described by the Hamiltonian (1), these energies are numerated by the number of electrons occupying impurity level, i.e.  and the atomic Green’s function takes a simple form

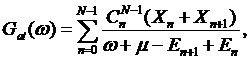                                                                                                                               (3)

where  are the probabilities to find an atom in configuration with  electrons while combinatorial factor  appear due to equivalence of all states with  electrons in .

We can represent the atomic Green’s function (3) using the rational representation (2), i.e.

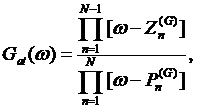                                                                                                                                             (4)

where  are all  atomic poles, while  denote  zeroes with  being the total degeneracy. The centers of the Hubbard bands are thus located at the atomic excitations . Using standard expression for the atomic Green’s function , we arrive to a desired representation for the atomic self–energy

                                                                                                                  (5)

 

Using this functional form for finite  modifies the positions of poles and zeroes via recalculating probabilities  which is equivalent to the famous Hubbard I approximation.

We now concentrate on the description of the quasiparticle peak which is present in metallic state of the system. For this an extra pole and zero have to be added in Eq (5). To see this, let us consider the Hubbard model for the  case where the local Green’s function can be written by the following Hilbert transform  If self–energy lifetime effects are ignored, the local spectral function becomes  where  is the non–interacting density of states. The peaks of the spectral functions thus appear as zeroes in Eq. (5) and in order to add the quasiparticle peak, one needs to add one extra zero (denoted hereafter as  to the numerator in Eq. (5). To make the self–energy finite at  one has to also add one more pole (denoted hereafter as ) which should appear in the denominator or Eq. (5). Furthermore, frequently the Hartree Fock value for the self–energy can be computed separately and it is desirable to have a parameter in the functional form (5) which will allow us to fix . An obvious candidate to be changed is that self–energy pole in (5) which is closest to  equal zero. Let us denote this parameter as  and rewrite the denominator of (5) as 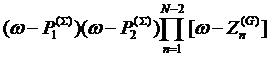 where the product is now extended over all zeroes of the atomic Green’s functions except the one closest to zero and two extra poles  and  can control the width of the quasiparticle peak and  Thus, we arrive to the functional form for the self–energy

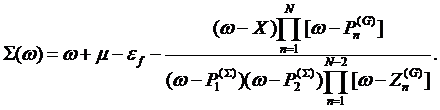                                                                                (6)

 

We are now ready to list all constrains of our interpolative scheme. To fix the unknown coefficients     in Eq. (6) and to write down the linear set of equations for the coefficients,  in Eq. (2) we use the following set of conditions.

a) Hartree Fock value  In the limit  the self–energy takes its Hartree–Fock form

                                                                                                                                                    (7)

Mean level occupancy is defined as a sum over all Matsubara frequencies for the Green’s function, i.e.

                                                                                                                                               (8)

where

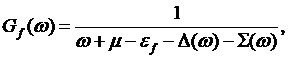                                                                                                                      (9)

defines the impurity Green’s function and  is the hybridization function.

b) Zero–frequency value  The so called Friedel sum rule establishes the relation between the total density and the real part of the self–energy at zero frequency

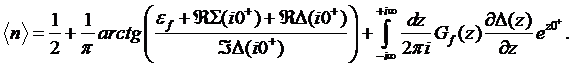                                            (10)

 

 

c) Quasiparticle mass renormalization value  The slope of the self–energy at zero frequency controls the quasiparticle residue,  using the following relationship

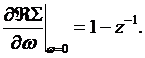                                                                                                                                                        (11)

Formally, constraints (b) and (c) hold for zero temperature only but we expect no significant deviations in many regions of parameters as long as we stay at low enough temperatures. The behavior may be more elaborated in the vicinity of Mott transition.

d) Positions of Hubbard bands.

As we discussed, in order that the self–energy obeys the atomic limit and places the centers of the Hubbard bands at the positions of the atomic excitations, we demand that

                                                                                                                                           (12)

This condition fixes almost all self–energy zeroes  in Eq.(2) to the poles  However, it alone does not ensure that the weight is correctly distributed among the Hubbard bands and that the very distant Hubbard bands disappear. For this to occur, distant poles of Green’s function have to be canceled out by nearby zeroes of the Green’s function. It is clear that each pole  far from the Fermi level has to be accompanied by a nearby zero  in order the weight of the pole be small. Thus, the self–energy has poles at the position of Green’s function zeroes which can be encoded into the constrain

                                                                                                                                                            (13)

We want to keep this property of the self–energy for finite  and thus demand that self–energy diverges (when lifetime effects are kept, it only reaches a local maximum) at the zeros of the functional form (3) of  Note that the relationship (13) holds (approximately) for frequency  larger than the renormalized bandwidth  Therefore the information about one  which lies close to  is omitted and replaced by the information about   and  as it is done by separating  and  in the denominator of Eq. (6).

We can now write down a set of linear equations for all unknown coefficients in the expression (2). There is total  of parameters  and  where we can always set  The conditions a),b),c) give

                                                                                                                                                                      (14)

                                                                                                                                                                              (15)

                                                                                                                                                  (16)

                                                                                                                                                        (17)

 

According to condition d) we can use all  poles  and  zeroes  The zero  closest to  is dropped out. This brings additional  equations for the coefficients and makes  as the degree of the rational interpolation which are written below

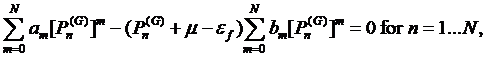                                                                  (18)

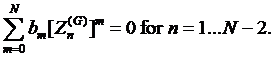                                                                                                                       (19)

 

 

Note that while  may be rather large, the actual number of poles contributing to the self–energy behavior is indeed very small. We can directly see this from Eq. (5) which uses all  poles  fulfilling Eq. (12) and uses  zeroes  directly related to  poles  Clearly, when the spectral weight of the atomic excitation becomes small, the corresponding  becomes close to  and the cancellation occurs. Therefore in realistic situations when only the upper and lower Hubbard bands have significant spectral weight along with the quasiparticle peak, the actual degree of the polynomial expansion is either two or three. However, it is advantageous numerically and cheap computationally to keep all poles and zeroes in Eq. (6) because the formula automatically distributes spectral weight over all existing Hubbard bands.

In the limit when  the self–energy automatically translates to the non–interacting one. The atomic poles get close to each other but, most importantly, their spectral weight goes rapidly to zero as it gets accumulated within the quasiparticle band.

In the Mott insulating regime, the conditions b) and c) drop out while all poles  and zeroes  can be used to determine the interpolation. However, in this regime it does not matter whether one of  closest to  is dropped out or kept, since we can always replace this information by information about  Therefore the Mott transition can be studied without changing the constraints.

We thus see that in the insulating case the self–energy correctly reproduces the well–known result of the Hubbard I method where the Green’s function is computed after Eq. (9) with atomic self–energy. If the lifetime effects are computed, the parameters  and  become complex and the Hubbard bands will acquire an additional bandwidth. This effect is evident from the simulations using various perturbative or QMC impurity solvers and can be in principle incorporated into the interpolative formulas (2) or (6). However, in in the current implementation we omit it for simplicity.

We thus see that the interpolational scheme is defined completely once a prescription for obtaining parameters such as   as well as poles , and zeroes  is given. For this purpose we will test two commonly used methods: SBMF method due to Gutzwiller [1] as described by Kotliar and Ruckenstein [2] and the well–known Hubbard I approximation [3]. We compare these results against more accurate but computationally demanding quantum Monte Carlo calculations and establish the procedure to extract all necessary parameters.

Note that once the constraints such as  are computed from a given approximate method, some of the quantities such as the total number of particles, , and the value of the self–energy at zero frequency,  can be computed fully self–consistently. They can be compared with their non–self–consistent values. If the approximate scheme already provides a good approximation for  and satisfies the Friedel sum rule, the self–consistency can be avoided hence accelerating the calculation. Indeed we found that inclusion of the self–consistency improves the results only marginally except when we are in a close vicinity to the Mott transition but here we do not expect that our simple interpolative algorithm is very accurate.

 

 [1] M. Gutzwiller, Phys. Rev. 134, A923 (1964).

[2] G. Kotliar and A. E. Ruckenstein, Phys. Rev. Lett. 57, 1362 (1986).

[3] J. Hubbard, Proc. Roy. Soc. (London) A281, 401 (1964).

Running program

·                 Compile program typing "make" at the source files location. Makefile was tested on Linux OS using PGI compiler. Please adjust it depending on operating system and compiler used.

·                 Edit “input" file which has the following structure:

 

1

IMOD 

0.0

EF 

2.0

U 

0.016

TEMP 

4

NDEG

500

NMSB

500

OMAX 

500

NOMG

50

WEND 

F

COMPUTE_REAL

 

where IMOD = 1 is the Hubbard Model, IMOD=3 the Anderson impurity model, EF is the impurity level, U is value of Coulomb repulsion, TEMP is temperature to be used used to create for Matsubara points grid, NDEG is the degeneracy, NMSB is the number of Matsubara point, OMAX is the imaginary frequency cutoff, NOMG is the number is real frequency points, WEND is the real frequency cutoff, COMPUTE_REAL is flag once is “True" tell program to produce the self-consistent solution (last iteration) on real axis.

1.               Program’s input consists from one more file (provided the Anderson impurity model item is chosen in “input" file):

“delta.dat" containing the hybridization function.

The structure is the following:

 

Column #

Value 

1

Frequency 

2

Re Delta 

3

Im Delta 

 

2.               Run the program executable (“main" is the default name).

3.               Program’s output consists from the following files:

1) “gfsig_iw.dat" containing Green’s function (GF) and the self-energy (SE) on Matsubara axis

2) “gfsig_re.dat" containing Green’s function (GF) and the self-energy (SE) on real axis provided flag "COMPUTE_REAL" is “TRUE".

They have the same structure:

 

Column #

Value 

1

Frequency 

2

Re GF 

3

Im GF 

4

Re SE 

5

Im SE 

 

3) “grid_re.dat" containing real frequency grid for the hybridization function (delta).

4) “grid_im.dat" containing Matsubara frequency grid for the hybridization function (delta).

Both files have the same structure:

 

Column #

Value 

1

Frequency 

 

Program content

 

Makefile

main make file 

dmf_cmpdiag.f

The solution of the generalized eigenvalue problem 

imp_sunatm.f

Solves Anderson impurity model, returns GF and SE. 

imp_sunmas.f

Computes effective mass renormalization

imp_sunrat.f

Finds rational interpolation or self-energy

lib_broy6.f

Broyden mixing.   

lib_cinv.f

Finds inverse of square matrix. 

lib_csplines.f

Splines complex function from one to another grid. 

lib_deriv1.f

Calculates radial derivative. 

lib_morefun.f

Calculations of a few auxiliary functions 

lib_pade.f

Realization of Pбde procedure. 

lib_pcoefs.f

Finds poles

lib_pzeros.f

Finds zeros

lib_simq.f

 Finds solution of a set of linear equations

lib_splin3.f

Computed a natural spline approximation of third order. 

mod_common.f

File containing common modules used across the program. 

mod_dimart.f

File containing common modules used across the program. 

mod_init.f

File containing common modules used across the program. 

sun.f

Main program.