Extracting LDA band structure parameters

To calculate transport parameters, including the optical conductivity as well as to calculate the photoemission spectra one needs make momentum summation of Green’s function (GF) or their convolutions. To do so one needs to make k-summation of DOS or the local Green’s function of a type:

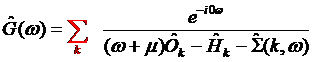
where is the chemical potential, is the overlap matrix, is the Hamiltonian and the is the self-energy matrix. In the LDA calculation the self-energy is represented by the Hartree-Fock constant while in the DMFT calculations it is frequency dependent function. Surely this integration/summation is the part of the LDA program we described in the previous section but very often it is quite convenient to have a separate routine/driver which does it outside one big program as it is much easier to change it in accord to a specific task.

But to make the summation we still use some information from LDA program i.e. the Hamiltonian, the overlap matrix, information about symmetry of a studied material. Program which prints all the necessary files for k-summation driver is the same as we described in the previous section with the only difference in printouts included. It means that one can make the self-consistent LDA calculation whether using this program or the previous one. And then one needs to make optical calculations to extract all the parameters. Run file should look something like this:

/home/user/LMTO/main <<!

latio3

ini+str+scs

scf+out

!

mv latio3.scf latio3.scs

mv latio3.out latio3.out_scf

/home/user/LMTO/main <<!

latio3

ini+str+scs

opt+out

!

mv latio3.out latio3.out_opt

(change /home/user/LMTO/ to the appropriate path to the program and latio3 to the studied material)

Once the program run one should get the following files as an output:

1. ham.dat	The Hamiltonian
2. olp.dat	The overlap
3. bz.dat	Brillouin zone data
4. grp.dat	Space group data
5. wig.dat	Space group data
6. idx.dat	Auxiliary index pointer
7. opar.dat	Factorization of the overlap
8. Sk.dat	Structure constants
9. vel.dat	Velocity matrix

1. Hamiltonian data (ham.dat).

This file contains the Hamiltonian matrix at each irreducible mesh point in the Brillouin zone. To facilitate and standardize the rotations of the Hamiltonian within the Brillouin zone the Hamiltonian is always assumed to be written in a spherical harmonics basis.

Quantity	Variable
Number of irreducible k-points	nkp
Dimension of Hamiltonian	ndim
Hamiltonian	hamf (1:ndim,1:ndim,1:nkp)

Table I:  Parameters available from ham.dat file.

Default energy unit on the Hamiltonian is Rydberg. Ndim=2 norb is the spin-orbital case is considered.

2. Overlap matrix data (olp.dat).

This file contains the overlap matrix at each irreducible mesh point in the Brillouin zone. The dimension of this matrix should be equal to the dimension of the Hamiltonian and the number of irreducible k-points should also match with the Hamiltonian data.

Quantity	Variable
Number of irreducible k-points	nkp
Dimension of overlap matrix	ndim
Overlap matrix	olap (1:ndim,1:ndim,1:nkp)

Table II: Parameters available from olp.dat file.

3. Brillouin zone data (bz.dat).

The file bz.dat contains the data on the Brillouin zone. It contains such information as the lattice constant, the mesh divisions, the irreducible k-points and tetrahedra as well as information about the group transformations that connect each k-point to its irreducible representative.

Quantity	Variable
Lattice constant	latcon
Number of irreducible k-points	nkp
Number of irreducible tetrahedra	ntet
Total number of k-points	nktot
Number of k-points along each direction	ndiv (1:3)
Coordinate array for irreducible k-points	bk (1:3,1:nkp)
Integration weight array for irreducible k-points	wk (1:nkp)
Pointer from each irreducible tetrahedron to its multiplicity, irreducible k-point corners and type	itt (1:6,1:ntet)
kcut matrices for all tetrahedron types (see Figure)	kcut (1:3,1:4,1:6)
Pointer from irreducible k-point to the four nearest irreducible neighbors in each direction	nbr (1:3,1:4,1:nkp)
Pointer from irreducible k-point to the group operation that rotates the irreducible neighbor to the real neighbor	grop (1:3,1:4,1:nkp)
Bravais lattice vectors, multiplied by the division along the reciprocal direction in Brillouin zone	rvec (1:3,1:3)
Brillouin zone minicell vectors (i.e. )	mvec (1:3,1:3)
Pointer from each mesh points to its irreducible representative	kirrptr (0:ndiv(1)-1,0:ndiv(2)-1, 0:ndiv(3)-1)
Pointer from each mesh point to the group operation that takes the irreducible representative to that point	gropptr (0:ndiv(1)-1,0:ndiv(2)-1, 0:ndiv(3)-1)

Table III. Parameters available from bz.dat file.

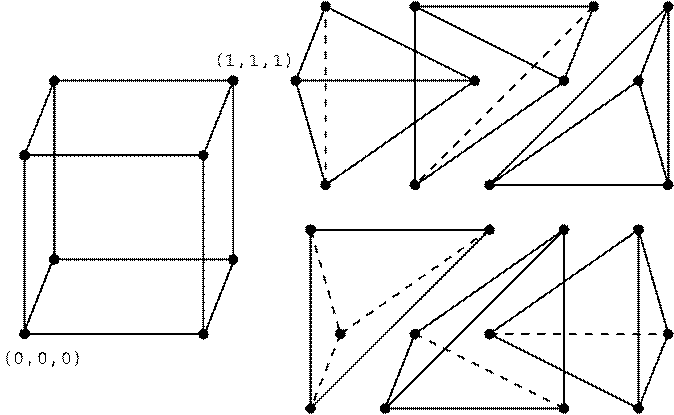
Figure I: One of four different ways of splitting the unit cube into six tetrahedral. The common diagonal is chosen from to . The coordinates of a given corner of each tetrahedron are given by the pointer kcut(m,,) where .

4. Group operations (grp.dat).

The file grp.dat contains information about the space group operations of the crystal. Here we read in both the number of atoms and the number of group operations that exist. In principle the maximum number of symmetry operations is 48 (cubic) but in low symmetry crystals they could be less and if one is using a reducible (i.e. not minimal) unit cell they could be more. To each of the symmetry operation corresponds a group operation element but since the maximum number of group elements is 48, two or more symmetry operations could correspond to a given group element. In addition to knowing the correspondence between the symmetry operations and the group elements one must know how the atoms move under the action of the symmetry operation if there are more than one atom of a given type in the unit cell. There is also the possibility that the symmetry operation takes the atom out of the unit cell and then it must be translated back by a lattice vector to the original unit cell. Since the Hamiltonian is in the Brillouin zone these translations must be known because they introduce phase factors into the equation for the transformation of the Hamiltonian.

Quantity	Variable
Number of symmetry operations	ngroup
Number of atoms in unit cell	natom
Symmetry operation to group element pointer	ikov (1:ngroup)
Atom to atom mapping for each symmetry operation	igatom (1:natom,1:ngroup)
Back to cell translation vectors for each atom and symmetry operation	rdc (1:3,1:natom,1:ngroup)

Table IV. Parameters available from grp.dat file.

5. Group operations (wig.dat).

The file wig.dat contains Wigner matrices for spherical harmonics angular momenta up to. This is needed to both rotate the Hamiltonian and the overlap matrix and to create the vector rotation matrices for each group operation. It contains \the number of group operations and the maximum angular momentum (should be always 3). The Wigner matrix is stored as a vector in the computer and the mapping from the angular momentum labels,, to the vector component, , is given by:

Quantity	Variable
Number of group operations	ng
Maximum angular momentum	lmax 3
Wigner matrices	wigmat (1:imax,1:48)

Table V. Parameters available from wig.dat file.

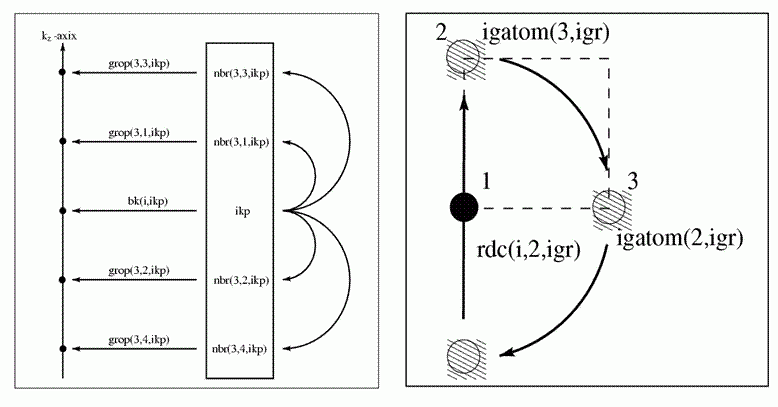
Figure II: Left figure: An illustration of the information encoded in the arrays nbr and grop along the 3rd () direction. Right figure: An illustration of the back-to-cell vectors rdc that take an atom that is rotated by the transformation igr out of the unit cell back to its equivalent position in the unit cell.

In addition to the parameters in Table V available from the file bz.dat there are two more parameters that are initialized using information in bz.dat. One of them is the total number of tetrahedra which is computed from the variable itt but should of course be equal to. The other one is a pointer from each corner of every tetrahedron to its irreducible representative.

Quantity	Variable
Total number of tetrahedra	mtet
Pointer from each tetrahedron corner to its irreducible representative	coridx (1:4,1:6,1:ndiv(1),1:ndiv(2),1:ndiv(3))

Table VI: Additional Parameters available initialized from data in bz.dat.

6. Auxiliary index data (idx.dat).

The file idx.dat contains pointers from the computer representation of the physical quantities (Hamiltonian etc.) as array to the corresponding atoms and angular momenta. Here we also get information about how many sorts of atoms there are, a pointer from each atom to its sort and what is the maximum angular momentum for a given atomic sort. We also have a logical array that indicates if some angular momenta are omitted from the Hamiltonian. This is useful if we want to consider simplified models where certain angular momenta have been ignored, usually because they are of much to low energy to be of interest.

Quantity	Variable
Number of atoms in unit cell	natom
Number of atomic sorts	nsort
Pointer from each atom to its sort	is (1:natom)
Pointer from each sort to its maximum angular momentum	ilsb (1:nsort)
Logical array indicating whether a given angular momentum is present for a given sort of atoms	ltpan (1:lmax,1:natom)
A pointer from each orbital state of every to its position in the Hamiltonian matrix	lmtind (1:(lmax+1),1:natom)

Table VII: Parameters available from idx.dat file.

7. Factorization of the overlap (opar.dat):

Files opar.dat and Sk.dat are used to orthonormalize (almost) the overlap matrix.

Quantity	Variable
Maximum angular momentum used	l_max
Number of atomic sorts	nsort
Number of spins	nspin (=2 for spin-orbit)
Transformation matrixes	moo(4,0:l_max,nsort,nspin)

Table VIII. Parameters available from opar.dat file.

8. Structure constants (Sk.dat):

The file Sk.dat contains the structure constants data.

Quantity	Variable
Maximum angular momentum used +1 squared	(l_max+1)
Number of atoms in unit cell	natom
Lattice constant	latcon
Structure constants	Stk(1:ndim,1:ndim,1:nkp)

Table VIII. Parameters available from Sk.dat file.

9. Velocity matrix (vel.dat).:

The vel.dat is the velocity matrix. It is not used in calculation of the k-integral. This information is used in the optical calculations.