Calculation of
DOS and Green’s function*
The definitions of the one-electron
Green’s function for interacting system is
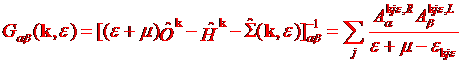(1.1)
where
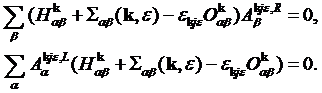
Here “L” denotes left eigenvector 
to distinguish it from the right “R” eigenvector
,
is the chemical potential, 
are the eigenvalues, 
is the self-energy, 
is the Hamiltonian
and 
is the overlap matrix
which takes into account the non-orthogonality of the basis set
,
and is defined as follows
.
The orthonormality condition is
,
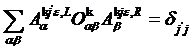or in the matrix form
.
Now one can easy see by inspection
that the Hamiltonian can be written in the form:
,
where 
is a diagonal matrix of eigenvalues. Using the above expression for the Hamiltonian
one can easily prove the above equation for the Green’s function:
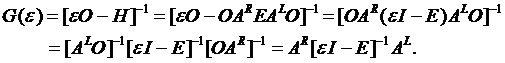
In direct space, formula for the Green’s
function is
,
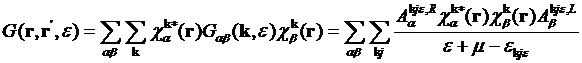or
,
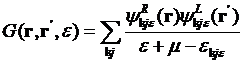where the wave functions are
,
which also satisfy to the following equations
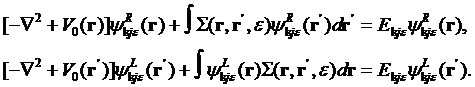
The Equation for the GF in direct space is
just the Fouriesr transformation of 
taking into account
the basis set equation:
.
Density can be found from the Green’s
function directly
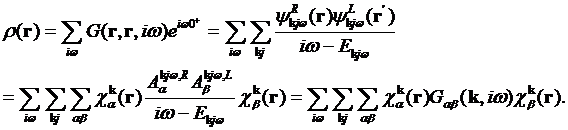
Integration over the space gives the interacting density matrix which should be
defined with the overlap matrix
,
in order to preserve the sum rule
related to the total number of electrons
.
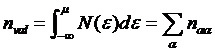Note, that as soon as we assume that
our basis set is orthonormal, we restore ordinary definitions for all the
relevant quantities discussed above.
The total density of states (TOS) is defined as
.
Unfortunately, the definition
,
has a problem since it does not have
proper symmetry transformation. By this we mean that
,
where 
are Wigner matrices
and
is
any group operation. Assuming by the rotation of the entire Brillouin zone
,
we see that we cannot prove this equality.
We can easily prove this for objects like
A possible way to resolve it can be found
if the overlap matrix can be represented as
(1.2)
where 
is the structure
constants and 
are the overlap
matices of Hankel and Bessel functions 
.
This representation is true in the Atomic
Sphere Approximation (ASA) only. If such factorization possible, we can define
the non-interacting density of states as
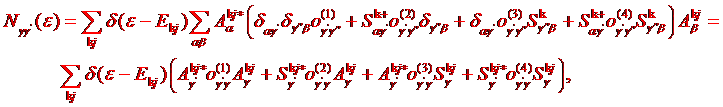(1.3)
where by 
we denoted
convolutions
.
It is clear
that each term obeys the required transformation property, and so does the
resulting 
Next we consider the basis
orthonormalization procedure. One can show that the overlap matrix can be
presented in the form
(1.4)
where we
made the following definitions
.
Here h and j are matrices which are
calculated by minimization such that Eq. (1.4) is best satisfied.
Let us
denote transformation 
which we use to bring
the system to the orthonormal basis
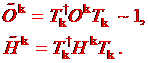(1.5)
In the almost
orthonormal basis the Green’s function reads as
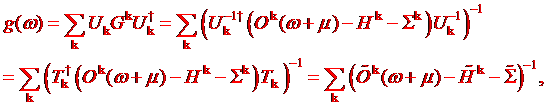(1.6)
where
(1.7)
Having GF g we can compute the density of states as
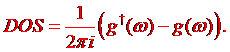(1.8)
Using GF and the self-energy
we can also compute the Weis GF using the following relation:
. (1.9)
The impurity levels can be obtained from the frequency expansion of the
impurity and local GFs:
, (1.10)
where matrix
contains
is the Hartree-Fock values of the self-energy, 
is the double counting term. As we see to
compute the impurity levels we need to know the following averages (which are
matrixes): 
.
If we are interested only in diagonal elements of the impurity matrix then the
expression (1.10) is simplified to
, (1.11)
where values of 
are provided by the
k-sum driver/program.
* Most of the equations
in the text related to LMTO ASA method can be found in
O. K. Andersen, Linear methods in band theory, Phys. Rev. B 12, 3060 (1975).
Last updated @ Sept 6 2004