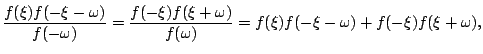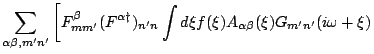 |
|||
![$\displaystyle \left.\qquad+
(F^{\b\dagger})_{mm^{\prime}}F^{\alpha }_{n^\prime n}\int d\xi
f(-\xi) A_{\b\alpha }(\xi)G_{m^\prime n^\prime}(i\omega-\xi)\right].$](img4.png) |
(1) |
The NCA diagrams correspond to the following analytic expression for the pseudoparticle self-energy
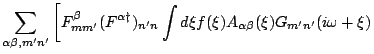 |
|||
![$\displaystyle \left.\qquad+
(F^{\b\dagger})_{mm^{\prime}}F^{\alpha }_{n^\prime n}\int d\xi
f(-\xi) A_{\b\alpha }(\xi)G_{m^\prime n^\prime}(i\omega-\xi)\right].$](img4.png) |
(1) |
To simplify the equations, we will write them in terms of spectral
quantities instead of Green's functions. Let us define
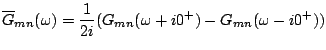 |
(3) | ||
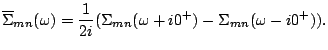 |
(4) |
With the above definitions, the NCA equations simplify to
The local electron Green's function within NCA approximation is given
by
![$\displaystyle G_{\alpha \b }(i\omega)=-\sum_{mnm^\prime n^\prime}F^{\alpha }_{n...
...}(\xi+i\omega)-G_{m^\prime
n^\prime}(\xi-i\omega)\overline{G}_{nm}(\xi)\right],$](img19.png) |
(6) |
Let me pause here for a moment and show that the
equations are invariant with respect to
the shift of frequency in the pseudo particle quantities due to local
gauge symmetry, therefore ![]() that appears in the definition of
the pseudo Green's functions can be an arbitrary number. In numerical
evaluation, we use this to our advantage and choose zero frequency at
the point where pseudo particle spectral functions diverge.
First, we want to show that shift of frequency arguments of all
pseudo-particle quantities by
that appears in the definition of
the pseudo Green's functions can be an arbitrary number. In numerical
evaluation, we use this to our advantage and choose zero frequency at
the point where pseudo particle spectral functions diverge.
First, we want to show that shift of frequency arguments of all
pseudo-particle quantities by
![]() does not affect the
equations provided that
does not affect the
equations provided that ![]() also changes to
also changes to
![]()
| (9) | |||
![$\displaystyle \overline{\Sigma}_{mn}(\omega+\delta\lambda)=
\sum_{\alpha \b ,m^...
...F^{\b\dagger})_{mm^{\prime}}F^{\alpha }_{n^\prime n}
A_{\b\alpha }(-\xi)\right]$](img27.png) |
(10) | ||
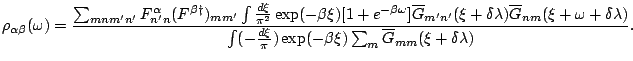 |
(11) |
In numerical evaluation, we can either fix ![]() and calculate
and calculate
![]() , or alternatively, fix
, or alternatively, fix ![]() and calculate
and calculate ![]() at each
iteration. The goal is to resolve the structure of the pseudo-particle
functions and therefore it is best to choose the zero frequency at the
point where the pseudo-quantities have a threshold (they diverge at
zero temperature). In the program, user can fix
at each
iteration. The goal is to resolve the structure of the pseudo-particle
functions and therefore it is best to choose the zero frequency at the
point where the pseudo-quantities have a threshold (they diverge at
zero temperature). In the program, user can fix ![]() to an arbitrary
number and the corresponding
to an arbitrary
number and the corresponding ![]() , which is just the impurity
free energy, is calculated. This guarantees that in zero temperature
limit the threshold point is at zero frequency. For small number of
local states, like for the one band model, the choice
, which is just the impurity
free energy, is calculated. This guarantees that in zero temperature
limit the threshold point is at zero frequency. For small number of
local states, like for the one band model, the choice ![]() is
best. When the number of bands grows,
is
best. When the number of bands grows, ![]() should grow as well. A good
choice is
should grow as well. A good
choice is
![]() where
where ![]() is the number of all
local states.
is the number of all
local states.
The above NCA equations are still numerically intractable because of
exponential factors appearing in Eq. (7) and (8). As we
mentioned, the pseudo-quantities have a threshold, i.e., they
exponentially vanish below a certain frequency (which is zero
frequency if ![]() is a fixed constant). However, the exponential tails
obviously enter the equation Eq. (7) and need to be
calculated. The problem can be circumvented by defining new quantities
that coincide with the original quantities above the threshold, but are
nonzero also below the threshold and carry the information needed below
the threshold. We will use the tilde sign for those new quantities
is a fixed constant). However, the exponential tails
obviously enter the equation Eq. (7) and need to be
calculated. The problem can be circumvented by defining new quantities
that coincide with the original quantities above the threshold, but are
nonzero also below the threshold and carry the information needed below
the threshold. We will use the tilde sign for those new quantities
| (12) | |||
| (13) |