Next: How to generate the
Up: Details of NCA evaluation
Previous: Details of NCA evaluation
Most of the Green's functions and specially Fermi function at low
temperature are very steep or peaked at certain points (usualy around
zero). The use of equidistant mesh is therefore impractical and time
consuming, rather a non-equidistant mesh is desired. We usualy use
logarithmic mesh at low frequency and tanges mesh at high frequnecies
to resolve almost any function with less than 300 points. The prices
one needs to pay using nonequidistant mesh is that a convolution like
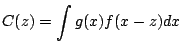 |
(17) |
is much harder to calculate since it is not resolved on the first mesh
neither on the second. Suppose that 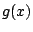 is defined on a certain
mesh
is defined on a certain
mesh 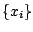 where it is resolved
where it is resolved
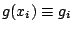 and function
and function
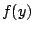 is defined on another mesh
is defined on another mesh 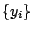 , i.e.,
, i.e.,
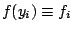 ,
the convolution can be safely calculated on the union of both mashes
,
the convolution can be safely calculated on the union of both mashes
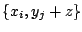 . One of the meshes should be shifted for
. One of the meshes should be shifted for 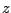 , thus for
each outside frequency a different union of the two meshes should be
formed and only then the convolution can be safely evaluated. This is
very time consuming and seldom done in practice.
, thus for
each outside frequency a different union of the two meshes should be
formed and only then the convolution can be safely evaluated. This is
very time consuming and seldom done in practice.
We have two strategies to circumvent the problem. If one knows that
both functions are peaked around certain point, lets suppose zero
frequency, we can form a two-dimensional mesh (somewhere in the
outside loop such that it is heavily reused) in which the first mesh
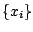 is superposed with couple of points around zero frequency
from mesh
is superposed with couple of points around zero frequency
from mesh  .
.
However, when a certain function needs to be convolved with many other
functions (typical case is NCA with many nonequivalent
pseudo-particles), one can use a trick. With the help of two
additional precalculated functions, the integral and first moment
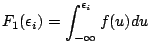 |
|
|
(18) |
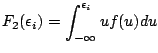 |
|
|
(19) |
one can calculate the convolution without building a new inside mesh.
Lets use the mesh 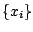 which resolves function
which resolves function 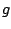 . Then, in the
spirit of trapezoid rule, we can lineraly interpolate
. Then, in the
spirit of trapezoid rule, we can lineraly interpolate 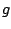 between the
points
between the
points
![$\displaystyle C(z)=\sum_i \int_{x_i}^{x_{i+1}}
\left[g_i+\frac{g_{i+1}-g_i}{x_{i+1}-x_i}(x-x_i)\right]f(x-z)dx.$](img53.png) |
(20) |
This integral can be expressed by the above defined functions. To show
that, let us rewrite the convolution and expressed it by the new
function
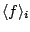 which is defined on the same mesh as
which is defined on the same mesh as 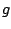 and with which the covolution is a simple scalar product
and with which the covolution is a simple scalar product
![$\displaystyle C(z)=\sum_i g_i\left[
\int_{x_i-z}^{x_{i+1}-z}\frac{x_{i+1}-z-u}...
...{i-1}}{x_{i}-x_{i-1}}f(u)du
\right]\equiv \sum_i g_i \langle f\rangle_i dh_i .$](img55.png) |
(21) |
Thus
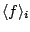 is
is
This method is specially suitable if function 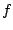 needs to be
convolved with many different functions that live on the same mesh
needs to be
convolved with many different functions that live on the same mesh
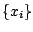 because the function
because the function
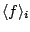 can be calculated
ones and reused many times. This is the case of NCA with many
nonequivalent local states. The method is also crucial for
implementing higher-order vertex correction to NCA.
The implementation can be found in the header file average.h.
can be calculated
ones and reused many times. This is the case of NCA with many
nonequivalent local states. The method is also crucial for
implementing higher-order vertex correction to NCA.
The implementation can be found in the header file average.h.
Next: How to generate the
Up: Details of NCA evaluation
Previous: Details of NCA evaluation
Kristjan Haule
2004-08-23
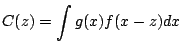
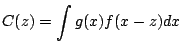
![]() is superposed with couple of points around zero frequency
from mesh
is superposed with couple of points around zero frequency
from mesh ![]() .
.
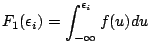
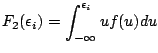
![$\displaystyle C(z)=\sum_i \int_{x_i}^{x_{i+1}}
\left[g_i+\frac{g_{i+1}-g_i}{x_{i+1}-x_i}(x-x_i)\right]f(x-z)dx.$](img53.png)
![$\displaystyle C(z)=\sum_i g_i\left[
\int_{x_i-z}^{x_{i+1}-z}\frac{x_{i+1}-z-u}...
...{i-1}}{x_{i}-x_{i-1}}f(u)du
\right]\equiv \sum_i g_i \langle f\rangle_i dh_i .$](img55.png)
![$\displaystyle \langle f\rangle_i=
\frac{2}{x_{i+1}-x_{i-1}}\left[
\int_{x_i-z}^...
...(u)du +
\int_{x_{i-1}-z}^{x_i-z}\frac{z+u-x_{i-1}}{x_{i}-x_{i-1}}f(u)du
\right]$](img56.png)
![$\displaystyle =
\frac{2}{x_{i+1}-x_{i-1}}\left[
\frac{(x_{i+1}-z)[F_1(x_{i+1}-z)-F_1(x_i-z)]-F_2(x_{i+1}-z)+F_2(x_i-z)}{x_{i+1}-x_i}-
\right.$](img57.png)
![$\displaystyle \left.-
\frac{(x_{i-1}-z)[F_1(x_i-z)-F_1(x_{i-1}-z)]-F_2(x_i-z)+F_2(x_{i-1}-z)]}{x_{i}-x_{i-1}}
\right]$](img58.png)