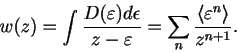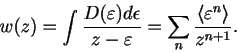Next: Running program
Up: hilbert
Previous: hilbert
Direct and inverse Hilbert transformations
Within DMFT, the real frequency self-energy can be obtained from
the local Green's function by the inversion of the Hilbert
transform. Although the implementation is very straightforward, we
will briefly mention the algorithm we used. In the high-frequency
regime, we can expand the Hilbert transform in terms of moments
of the DOS as
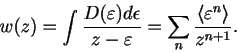 |
(1) |
The series can be inverted and solved for 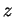
For most of the frequency points, the expansion up to some higher
power (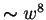 ) gives already an accurate estimation for the
inverse function. However, when
) gives already an accurate estimation for the
inverse function. However, when 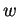 gets large, we need to use
one of the standard root-finding methods to accurately determine
the solution. This is however much easier than general
root-finding in complex plane since we always have a good
starting guess for the solution. We start evaluating the inverse
function at high frequency where the absolute value of
gets large, we need to use
one of the standard root-finding methods to accurately determine
the solution. This is however much easier than general
root-finding in complex plane since we always have a good
starting guess for the solution. We start evaluating the inverse
function at high frequency where the absolute value of 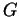 is
small and we can use the expansion in Eq. (2). Then
we use the fact that Green's function is a continuous function of
a real frequency and we can follow the solution from frequency
point to frequency point by improving it with few steps of a
secant (or Newton) method. A special attention, however, must be
paid not to cross the branch-cut and get lost in the non-physical
complex plane. Therefore, each secant or Newton step has to be
shortened if necessary. The self-energy is finally expressed by
the inverse of Hilbert transform
is
small and we can use the expansion in Eq. (2). Then
we use the fact that Green's function is a continuous function of
a real frequency and we can follow the solution from frequency
point to frequency point by improving it with few steps of a
secant (or Newton) method. A special attention, however, must be
paid not to cross the branch-cut and get lost in the non-physical
complex plane. Therefore, each secant or Newton step has to be
shortened if necessary. The self-energy is finally expressed by
the inverse of Hilbert transform 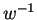 as
as
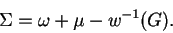 |
(3) |
Next: Running program
Up: hilbert
Previous: hilbert
Victor Oudovenko
2005-02-01